为了循序渐进,先从二维开始讲起,然后过渡到三维
1. 二维空间#
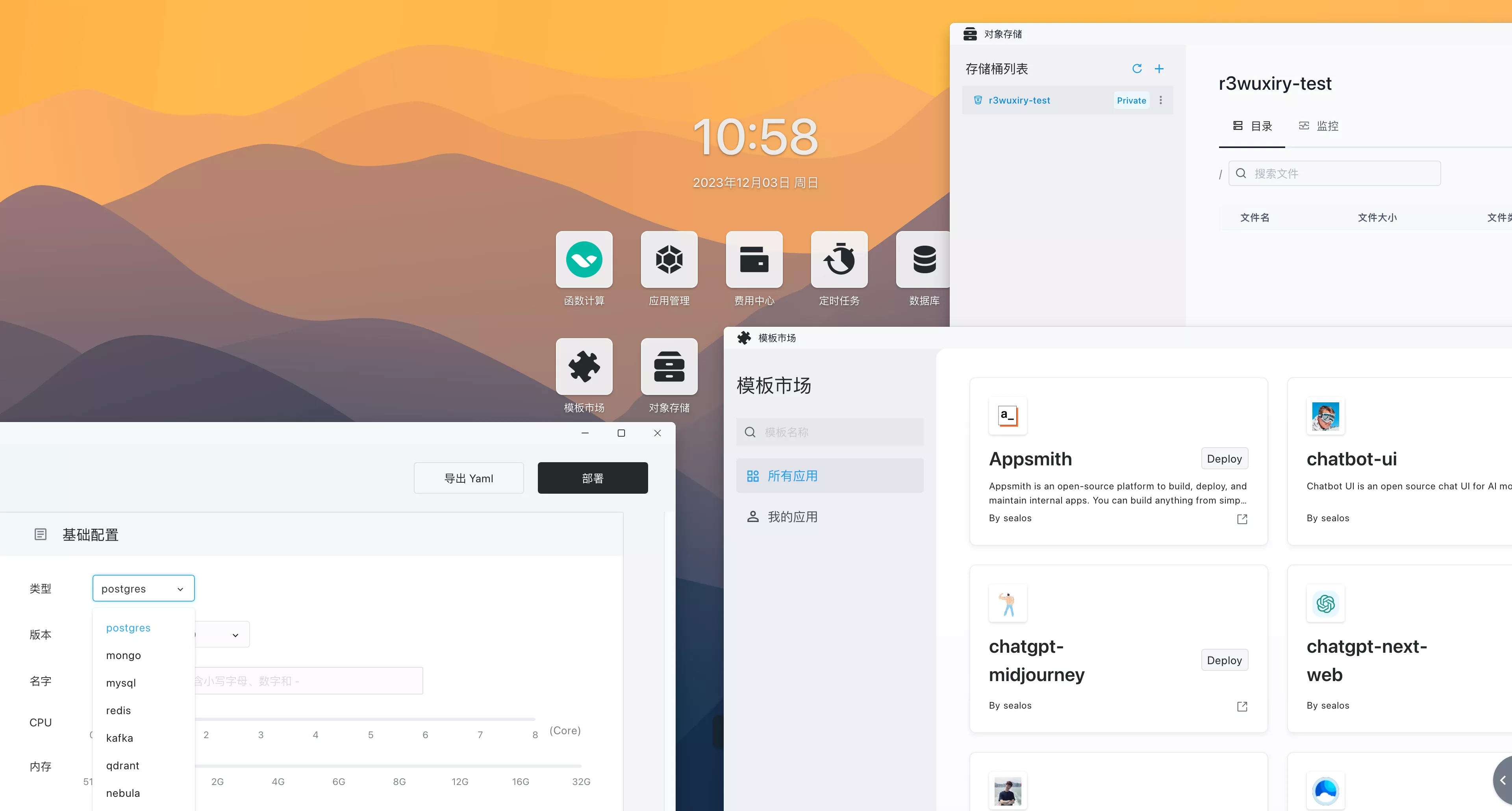
我们从一个五边形的面积开始说起
比如我们要求这个正五边形的面积,该怎样用向量求呢?
先简化这个问题,不用考虑五边形,只需考虑三角形。
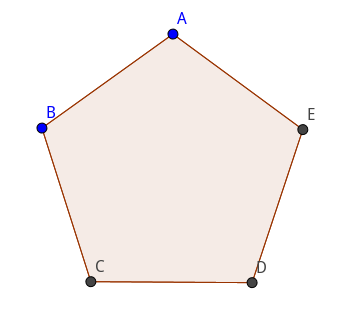
现在,我们把正五边形分割成三个三角形,再把三角形的面积加起来,就得到了五边形的面积。
那么问题来了:怎样求三角形的面积?
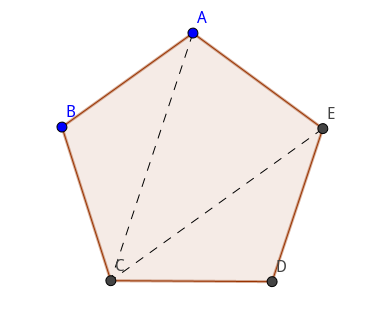
设三角形的面积为S,那么
$$ S = \frac{1}{2}\left|\vec{A}\right|\left|\vec{MN}\right| = \frac{1}{2}\left|\vec{A}\right|\left|\vec{B}\right|\sin(\theta) \tag{1} $$
$\sin(\theta)$ 该如何求呢?
如果你学过向量的点积,应该知道$\vec{a}\cdot\vec{b}=\left|\vec{a}\right|\left|\vec{b}\right|\cos(\theta)$.
所以为了求$\sin(\theta)$,我们可以先求出$\cos(\theta)$
$$ \cos(\theta)=\frac{\vec{a}\cdot\vec{b}}{\left|\vec{a}\right|\left|\vec{b}\right|} \tag{2} $$
再利用公式
$$ \cos^2(\theta)+\sin^2(\theta)=1 \tag{3} $$
便可以求出 $\sin(\theta)$ 的值。
通过以上步骤,可以看出这样做很麻烦,有没有更简单的办法呢?当然有
求 $\sin(\theta)$ 太麻烦了,但是求 $\cos(\theta)$ 却很简单,为了避免求 $\sin(\theta)$,我们能否找到一个角,使这个角的余弦等于 $\sin(\theta)$ ?
作向量$\vec{A}$、$\vec{B}$,夹角记为$\theta$,将向量$\vec{A}$逆时针旋转 $90^\circ$ 得到 $\vec{A^\prime}$,如下图所示:
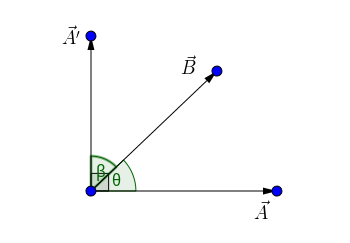
通过上图给的条件,我们已知:
$$ \begin{cases} \beta=\frac{\pi}{2}-\theta \\ \cos(\beta)=\sin(\theta) \end{cases} $$
这意味着$\vec{A}$的模长乘以$\vec{B}$的模长,再乘以$\sin(\theta)$,等于$\vec{A^\prime}$的模长乘以$\vec{B}$的模长,再乘以$\cos(\beta)$,得到:
$$ \begin{aligned} &\left|\vec{A}\right|\left|\vec{B}\right|\sin(\theta) \\ = &\left|\vec{A^\prime}\right|\left|\vec{B}\right|\cos(\beta) \\ = &\vec{A^\prime}\cdot\vec{B} \end{aligned} $$
即:
$$ \left|\vec{A}\right|\left|\vec{B}\right|\sin(\theta)=\vec{A^\prime}\cdot\vec{B} \tag{4} $$
这个方法看起来不错,不过还有一点是不知道的,就是怎么求$\vec{A^\prime}$呢?
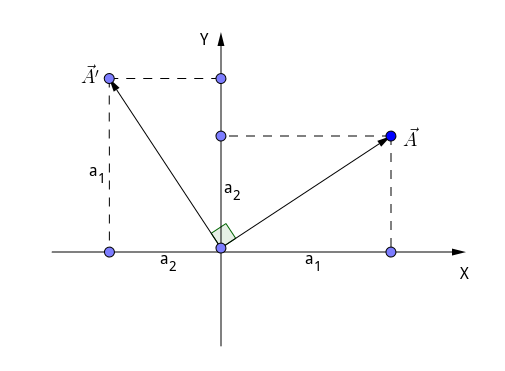
假设$\vec{A}$的坐标为$\left\langle a_1,a_2 \right\rangle$,由我画的图可知,逆时针旋转 $90^\circ$ 后,得到:$A^\prime=\left\langle -a_2,a_1 \right\rangle$ 。
同时再假设$\vec{B}$的坐标为$\left\langle b_1,b_2 \right\rangle$,现在将$\vec{A}$和$\vec{B}$的坐标分别带入(4)式,得到:
$$ \begin{aligned} & \vec{A^\prime}\cdot\vec{B} \\ = & \left\langle -a_2,a_1 \right\rangle \cdot \left\langle b_1,b_2 \right\rangle \\ = & a_1b_2-a_2b_1 \end{aligned} $$
如果你学过行列式,应该知道
$$ \begin{aligned} & a_1b_2-a_2b_1 \\ = & \begin{vmatrix} a_1 & a_2 \\\ b_1 & b_2 \end{vmatrix} \\ = & det(\vec{A},\vec{B}) \end{aligned} $$
由此可知,三角形的面积
$$ S=\frac{1}{2}det(\vec{A},\vec{B}) \tag{5} $$
现在可以得出结论:
向量$\vec{A}$与向量$\vec{B}$的行列式表示一个以$\vec{A}$和$\vec{B}$为边构成的平行四边形的面积
还可以表述得更严格一点,因为面积没有负数,而行列式的值有正有负,符号取决于两个向量之间的夹角,所以我们可以这样描述:
向量$\vec{A}$与向量$\vec{B}$的行列式的绝对值表示一个以$\vec{A}$和$\vec{B}$为边构成的平行四边形的面积
2. 三维空间#
在空间中,从简单的开始,我们可以做两件事情:
- 求平行六面体的体积
- 求平行六面体的表面积
咱们先来求平行六面体的体积。
平行六面体的体积#
求体积之前,需要了解几个定义
空间中的行列式#
空间中也有行列式的概念,假设有三个向量$\vec{A}$、$\vec{B}$和$\vec{C}$,定义:
$$ \begin{aligned} det(\vec{A},\vec{B},\vec{C}) & = \begin{vmatrix} a_1 & a_2 & a_3 \\\ b_1 & b_2 & b_3 \\\ c_1 & c_2 & c_3 \end{vmatrix} \\ & = a_1\begin{vmatrix} b_2 & b_3 \\\ c_2 & c_3 \end{vmatrix} - a_2\begin{vmatrix} b_1 & b_3 \\\ c_1 & c_3 \end{vmatrix} + a_3\begin{vmatrix} b_1 & b_2 \\\ c_1 & c_2 \end{vmatrix} \end{aligned} $$
如果你学过行列式的知识,上面的计算过程应该很容易理解,我就不作过多解释了。
叉乘#
叉乘适用于两个在空间内的向量(这里我指的是三维空间),定义:
$$ \begin{aligned} \vec{A}\times\vec{B}=\begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\\ a_1 & a_2 & a_3 \\\ b_1 & b_2 & b_3 \end{vmatrix} \end{aligned} $$
其中,$\hat{i}$,$\hat{j}$,$\hat{k}$分别为三维空间中的三个坐标轴上的单位向量。
我们把$\vec{A}\times\vec{B}$称为向量$\vec{A}$与$\vec{B}$的叉乘!
如果你仔细观察,你会发现,这个行列式的第二行和第三行分别是向量$\vec{A}$和$\vec{B}$的坐标,但是第一行却是三个单位向量,这意味着后面两行的元素都是数值,而第一行的元素都是向量。这意味着什么?这不是常理上的行列式,如果你尝试在计算器中这样计算,它会显示这是错误的,向量不该出现在这里。
那么,为什么要这么做呢?
如果使用上面提到的空间中的行列式的定义,可以得到:
$$ \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix} = \begin{vmatrix} a_2 & a_3 \\ b_2 & b_3 \end{vmatrix}\hat{i} - \begin{vmatrix} a_1 & a_3 \\ b_1 & b_3 \end{vmatrix}\hat{j} + \begin{vmatrix} a_1 & a_2 \\ b_1 & b_2 \end{vmatrix}\hat{k} \tag{6} $$
你发现了什么?没错,我们得到的结果不是一个数,而是一个向量,这就是向量叉乘的定义。
那么问题在于,这样定义有什么好处呢?这种怪异计算的几何意义在哪里?为什么我们要费心去这样做?
下面我们对上面的式子进行转化,看看会出现什么神奇的结果。
将式(6)进一步化简,得到:
$$ \begin{aligned} \vec{A}\times\vec{B}=(a_2b_3-a_3b_2)\hat{i}-(a_1b_3-a_3b_1)\hat{j}+(a_1b_2-a_2b_1)\hat{k} \end{aligned} $$
看起来没什么特别的,试着求一下$\vec{A}\times\vec{B}$的模,为了方便计算,我们求$\vec{A}\times\vec{B}$的模的平方
$$ \begin{aligned} \left| \vec{A}\times\vec{B} \right|^2 & = (a_2b_3-a_3b_2)^2 + (a_1b_3-a_3b_1)^2 + (a_1b_2-a_2b_1)^2 \\ & = (a_1^2b_2^2+a_1^2b_3^2) + (a_2^2b_1^2+a_2^2b_3^2) + (a_3^2b_1^2+a_3^2b_2^2) \\ & - 2(a_1a_2b_1b_2+a_1a_3b_1b_3+a_2a_3b_2b_3) \\ & = (\underbrace{a_1^2b_2^2+a_1^2b_3^2}+a_1^2b_1^2) + (\underbrace{a_2^2b_1^2+a_2^2b_3^2}+a_2^2b_2^2) + (\underbrace{a_3^2b_1^2+a_3^2b_2^2}+a_3^2b_3^2)i - (a_1^2b_1^2+a_2^2b_2^2+a_3^2b_3^2) - 2(a_1a_2b_1b_2+a_1a_3b_1b_3+a_2a_3b_2b_3) \\ & = {(\underbrace{a_1^2b_1^2+a_1^2b_2^2+a_1^2b_3^2) + (a_2^2b_1^2+a_2^2b_2^2+a_2^2b_3^2) + (a_3^2b_1^2+a_3^2b_2^2+a_3^2b_3^2)}} - {\underbrace{(a_1^2b_1^2+a_2^2b_2^2+a_3^2b_3^2) + 2(a_1a_2b_1b_2+a_1a_3b_1b_3+a_2a_3b_2b_3)}} \\ & = (a_1^2+a_2^2+a_3^2)(b_1^2+b_2^2+b_3^2) - (a_1b_1+a_2b_2+a_3b_3)^2 \\ & = \left|\vec{A}\right|^2\cdot\left|\vec{B}\right|^2-\left|\vec{A}\cdot\vec{B}\right|^2 \\ & = \left|\vec{A}\right|^2\cdot\left|\vec{B}\right|^2\cdot1-\left|\vec{A}\right|^2\cdot\left|\vec{B}\right|^2\cdot\frac{\left|\vec{A}\cdot\vec{B}\right|^2}{\left|\vec{A}\right|^2\cdot\left|\vec{B}\right|^2} \\ & = \left|\vec{A}\right|^2\cdot\left|\vec{B}\right|^2(1-\frac{\left|\vec{A}\cdot\vec{B}\right|^2}{\left|\vec{A}\right|^2\cdot\left|\vec{B}\right|^2}) \\ & = \left|\vec{A}\right|^2\cdot\left|\vec{B}\right|^2(1-cos^2\left\langle\vec{A},\vec{B}\right\rangle) \\ & = (\left|\vec{A}\right|\cdot\left|\vec{B}\right|\cdot\sin\left\langle\vec{A},\vec{B}\right\rangle)^2 \end{aligned} $$
发现了什么?原来$\vec{A}\times\vec{B}$的模长等于一个以$\vec{A}$和$\vec{B}$为边构成的平行四边形的面积。
接下来的问题是:既然$\vec{A}\times\vec{B}$的结果是一个向量,那么这个向量的方向是什么呢?
答案是:它的方向垂直于向量$\vec{A}$与$\vec{B}$构成的平面,并且遵循右手定则。
如果你不知道右手定则,我可以解释一下:
首先,你的右手平行于向量 $\vec{A}$ 的方向,然后,你的手指向向量 $\vec{B}$ 的方向弯曲,这时,你的大拇指竖直的方向就是 $\vec{A}\times\vec{B}$ 的方向。
下面我们来证明一下为什么$\vec{A}\times\vec{B}$的方向垂直于向量$\vec{A}$与$\vec{B}$构成的平面。
为了简化,令
$$ \begin{cases} m_1=a_2b_3-a_3b_2 \\ m_2=a_1b_3-a_3b_1 \\ m_3=a_1b_2-a_2b_1 \end{cases} $$
于是可以得到
$$ \vec{A}\times\vec{B}=m_1\hat{i}-m_2\hat{j}+m_3\hat{k} \tag{7} $$
基本思路是这样 :** 我们从$\vec{A}$与$\vec{B}$构成的平面中找两个方向不在同一条直线上的向量,如果$\vec{A}\times\vec{B}$与这两个向量均垂直,那么它就垂直于$\vec{A}$与$\vec{B}$构成的平面**
为了方便计算,我们这样定义三个互相垂直的单位向量:其中,向量$\hat{i}$与$\hat{j}$在$\vec{A}$与$\vec{B}$构成的平面上,而向量$\hat{k}$垂直于这个平面。
现在问题简单了,只要我们能证明$\hat{i}\times\hat{j}$的方向平行于$\hat{k}$,就说明$\vec{A}\times\vec{B}$的方向垂直于向量$\vec{A}$与$\vec{B}$构成的平面。
设 $\hat{i}=\left\langle1,0,0\right\rangle$,$\hat{j}=\left\langle0,1,0\right\rangle$,$\hat{k}=\left\langle0,0,1\right\rangle$,那么
$$ \begin{aligned} \hat{i}\times\hat{j} & = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{vmatrix} \\ & = \begin{vmatrix} 0 & 0 \\ 1 & 0 \end{vmatrix}\hat{i}-\begin{vmatrix} 1 & 0 \\ 0 & 0 \end{vmatrix}\hat{j}+\begin{vmatrix} 1 & 0 \\ 0 & 1 \end{vmatrix}\hat{k} \\ & = \hat{k} \end{aligned} $$
太神奇了,$\hat{i}\times\hat{j}$竟然等于$\hat{k}$,所以当然也平行于$\hat{k}$,所以$\vec{A}\times\vec{B}$的方向垂直于向量$\vec{A}$与$\vec{B}$构成的平面,并且遵循右手定则。
于是可以得到如下的结论:
- $\left|\vec{A}\times\vec{B}\right|$等于一个以$\vec{A}$和$\vec{B}$为边构成的平行四边形的面积
- $\vec{A}\times\vec{B}$的方向垂直于向量$\vec{A}$与$\vec{B}$构成的平面,并且遵循右手定则
下面我们回到最初提出的问题 :** 求平行六面体的体积**
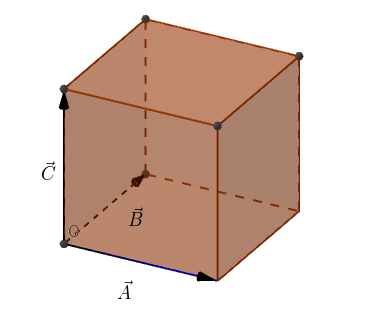
如上图所示,我们要求由三个向量 $\vec{A}$,$\vec{B}$ 与 $\vec{C}$ 构成的平行六面体的体积。
设体积为V,向量$\vec{A}$与$\vec{B}$构成的平行四边形的面积为S,高为h,那么:
$$ V=S \cdot h \tag{8} $$
通过上面的分析,可以得知$S=\left|\vec{A}\times\vec{B}\right|$,那么高度h该怎么求呢?
假设高度h的方向为$\vec{H}$,那么h等于向量$\vec{C}$在向量$\vec{H}$上的投影,所以
$$ \begin{aligned} h & = \left|\vec{C}\cdot\right|\cos\left\langle\vec{C},\vec{H}\right\rangle \\ & = \left|\vec{C}\right|\cdot\frac{\vec{C}\cdot\vec{H}}{\left|\vec{C}\right|\left|\vec{H}\right|} \\ & = \vec{C}\cdot\frac{\vec{H}}{\left|\vec{H}\right|} \\ & = \vec{C}\cdot\vec{h}, & \text{设$\vec{h}$为向量$\vec{H}$方向上的单位向量} \end{aligned} $$
带入(8)式,得:
$$ \begin{aligned} V & = \left|\vec{A}\times\vec{B}\right|\cdot(\vec{C}\cdot\vec{h}) \\ & = \left|\vec{A}\times\vec{B}\right|\cdot(\vec{C}\cdot\frac{\vec{A}\times\vec{B}}{\left|\vec{A}\times\vec{B}\right|}) \\ & = \vec{C}\cdot(\vec{A}\times\vec{B}) \\ & = \left\langle c_1,c_2,c_3 \right\rangle\cdot\lbrace(a_2b_3-a_3b_2)\hat{i} - (a_1b_3-a_3b_1)\hat{j} + (a_1b_2-a_2b_1)\hat{k}\rbrace \\ & = \left\langle c_1,c_2,c_3 \right\rangle\cdot\left\langle a_2b_3-a_3b_2,a_1b_3-a_3b_1,a_1b_2-a_2b_1 \right\rangle \\ & = c_1\begin{vmatrix} a_2 & a_3 \\ b_2 & b_3 \end{vmatrix} - c_2\begin{vmatrix} a_1 & a_3 \\ b_1 & b_3 \end{vmatrix} + c_3\begin{vmatrix} a_1 & a_2 \\ b_1 & b_2 \end{vmatrix} \\ & = det(\vec{A},\vec{B},\vec{C}) \end{aligned} $$
即:
$$ V=det(\vec{A},\vec{B},\vec{C})=\vec{C}\cdot(\vec{A}\times\vec{B}) \tag{9} $$
$\vec{C}\cdot(\vec{A}\times\vec{B})$ 称为向量的混合积。
现在可以得出结论:
向量$\vec{A}$、$\vec{B}$与$\vec{C}$的行列式等于由向量$\vec{A}$、$\vec{B}$与$\vec{C}$构成的平行六面体的体积
体积的部分暂时就讲到这里,接下来的一篇将会介绍平行六面体的面积。