为了弄明白子空间投影是怎么一回事,我们遵循从低维到高维的规律,先从二维开始讲起。
1. 二维空间#
如下图所示(我随手画的,不要介意),设向量p是向量b在向量a上面的投影,向量e垂直于向量p及a。
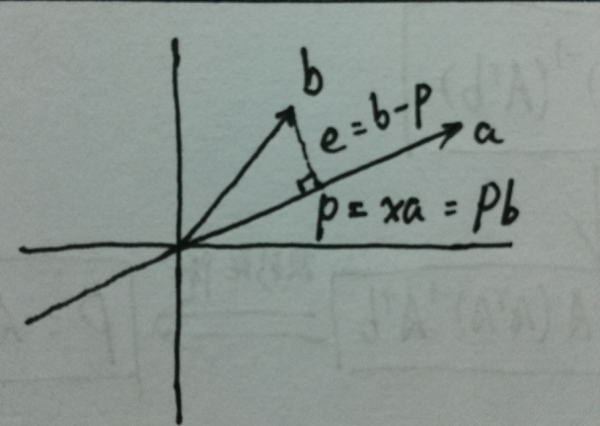
于是我们可以得到这样的一个等式:
$$ a^Te = 0 $$
即
$$a^T(b-xa) = 0\tag{1}$$
解得:
$$x = \frac{a^Tb}{a^Ta}$$
于是向量p可表示为:
$$p = xa = a\frac{a^Tb}{a^Ta}\tag{2}$$
现在我们设
$$p = Pb\tag{3}$$
我们把这个矩阵P称为投影矩阵。
比较式(2)和式(3),立即可以知道:
$${P = \frac{a \cdot a^T}{a^T \cdot a}}\tag{4}$$
2. 三维空间#
为了让你们能够有一个直观的认识,我仍然用我高超的画艺画了一幅美图:
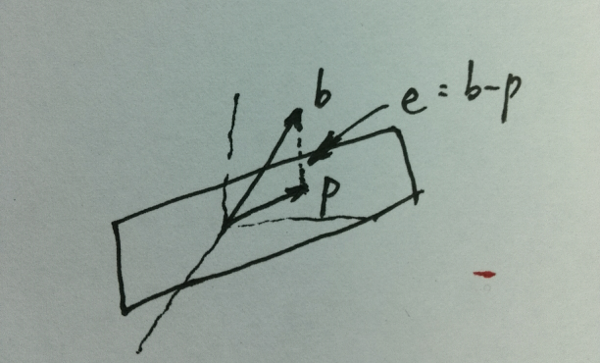
假设图中的那个平面由向量$a_1$和$a_2$构成,令
$$A = \begin{bmatrix} a_1 & a_2 \end{bmatrix}$$
由于向量p在平面上,所以p可以表示为:
$$p = \hat{x_1}a_1 + \hat{x_2}a_2\tag{5}$$
即
$$p = A\hat{x}\tag{6}$$
与二维空间类似,设向量p是向量b在平面上的投影,向量e垂直于那个平面,当然也垂直于向量p,同样也垂直于向量$a_1$和$a_2$,于是可以得到方程组:
$$ \begin{cases} a_1^T(b - A\hat{x}) = 0 \\ a_2^T(b - A\hat{x}) = 0 \\ \end{cases}\tag{7} $$
即
$$ \begin{bmatrix} a_1^T \\a_2^T \end{bmatrix}(b - A\hat{x}) = \begin{bmatrix} 0 \\0 \end{bmatrix} $$
进一步化简得到:
$$A^T(b - A\hat{x}) = 0\tag{8}$$
解得:
$$\hat{x} = (A^TA)^{-1}(A^Tb)\tag{9}$$
将(9)代入(6)得:
$$p = A\hat{x} = A(A^TA)^{-1}A^Tb\tag{10}$$
与二维空间类似,我们设
$$p = Pb\tag{11}$$
比较式(10)和式(11),立即可以得到:
$${P = A(A^TA)^{-1}A^T}\tag{12}$$
这就是投影矩阵的表达式!